Задачник Абрамова № 11

• Алексей
• Комментариев нет

§ 1. Арифметика действительных чисел. Вычисление по формулам.

11. Даны x, y, z. Вычислить а, b, если

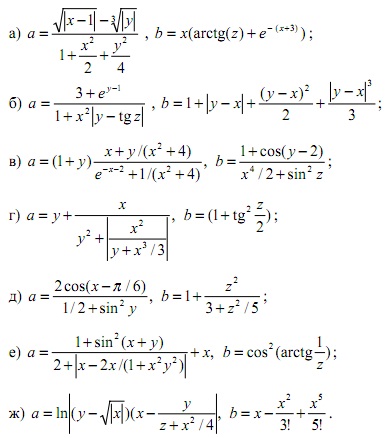
C:

#include <stdio.h>;
#include <math.h>

int fac(int n)
{
	return !n ? 1 : n * fac(n - 1);
}

int main()
{
	float x,y,z,a,b;
	const float pi = 3.14;
	printf("x = ");
	scanf("%f",&x);
	printf("y = ");
	scanf("%f",&y);
	printf("z = ");
	scanf("%f",&z);
	/*a*/
	a = (sqrt(fabs(x-1))-pow(fabs(y),1/3))/(1+x*x/2+y*y/4);
	b = x*(atan(z)+exp(-(x+3)));
	printf("a)na = %fnb = %fn",a,b);
	/*b*/
	a = (3+exp(y-1))/(1+x*x*fabs(y-tan(z)));
	b = 1+fabs(y-x)+pow((y-x),2)/2+pow((y-x),3)/3;
	printf("b)na = %fnb = %fn",a,b);
	/*v*/
	a = (1+y)*(x+y/(x*x+4))/(exp(-x-2)+1/(x*x+4));
	b = (1+cos(y-2))/(pow(x,4)/2+pow(sin(z),2));
	printf("v)na = %fnb = %fn",a,b);
	/*g*/
	a = y+x/(y*y+fabs(x*x/(y+pow(x,3)/3)));
	b = 1+pow(tan(z/2),2);
	printf("g)na = %fnb = %fn",a,b);
	/*d*/
	a = (2*cos(x-pi/6))/(1/2+pow(sin(y),2));
	b = 1 + z*z/(3+z*z/5);
	printf("d)na = %fnb = %fn",a,b);
	/*e*/
	a = (1+pow(sin(x+y),2))/(2+fabs(x-2*x/(1+x*x*y*y)));
	b = pow(cos(atan(1/z)),2);
	printf("e)na = %fnb = %fn",a,b);
	/*j*/
	a = log(fabs((y-sqrt(fabs(x)))*(x-y/(z+x*x/4))));
	b = x-x*x/fac(3)+pow(x,5)/fac(5);
	printf("j)na = %fnb = %fn",a,b);
	return 0;
}

Pascal:

const pi = 3.14;
var x,y,z,a,b:real;

function pow(x,n:real):real;
var tmp:real;
begin
	tmp:= abs(x);
	if x < 0 then
		pow := (-1)*exp((n)*ln(tmp))
	else
		pow := exp((n)*ln(tmp));
end;

function fac(n:integer):longint;
begin
	if n <= 1 then
		fac := 1
    else
		fac := n*fac(n-1);
end;

function tan(x:real):real;
begin
	tan := sin(x)/cos(x)
end;

begin
	write('x = ');
	read(x);
	write('y = ');
	read(y);
	write('z = ');
	read(z);
	{a}
	a := (sqrt(abs(x-1))-pow(abs(y),1/3))/(1+x*x/2+y*y/4);
	b := x*(arctan(z)+exp(-(x+3)));
	write('a)',#13#10,'a = ',a:4:2,#13#10,'b = ',b:4:2,#13#10);
	{b}
	a := (3+exp(y-1))/(1+x*x*abs(y-tan(z)));
	b := 1+abs(y-x)+pow((y-x),2)/2+pow((y-x),3)/3;
	write('b)',#13#10,'a = ',a:4:2,#13#10,'b = ',b:4:2,#13#10);
	{v}
	a := (1+y)*(x+y/(x*x+4))/(exp(-x-2)+1/(x*x+4));
	b := (1+cos(y-2))/(pow(x,4)/2+pow(sin(z),2));
	write('v)',#13#10,'a = ',a:4:2,#13#10,'b = ',b:4:2,#13#10);
	{g}
	a := y+x/(y*y+abs(x*x/(y+x*x*x/3)));
	b := 1+pow(tan(z/2),2);
	write('g)',#13#10,'a = ',a:4:2,#13#10,'b = ',b:4:2,#13#10);
	{d}
	a := (2*cos(x-pi/6))/(1/2+pow(sin(y),2));
	b := 1 + z*z/(3+z*z/5);
	write('d)',#13#10,'a = ',a:4:2,#13#10,'b = ',b:4:2,#13#10);
	{e}
	a := (1+pow(sin(x+y),2))/(2+abs(x-2*x/(1+x*x*y*y)));
	b := pow(cos(arctan(1/z)),2);
	write('e)',#13#10,'a = ',a:4:2,#13#10,'b = ',b:4:2,#13#10);
	{j}
	a := ln(abs((y-sqrt(abs(x)))*(x-y/(z+x*x/4))));
	b := x-x*x/fac(3)+pow(x,5)/fac(5);
	write('j)',#13#10,'a = ',a:4:2,#13#10,'b = ',b:4:2,#13#10);
end.

Для обоих языков была разработана функция для поиска факториала fac(n), в качестве аргумента она принимает целое число, возвращает факториал этого числа. Для Pascal были разработаны отсутствующие в данном языке функции для возведения числа в степень и вычисления тангенса числа. Первая функция function pow(x,n:real):real в качестве аргументов принимает два вещественных числа x и n, вовращает число x возведенное в степень n. Вторая функция function tan(x:real):real в качестве аргумента принимает вещественное число и возвращем тангенс этого числа.